quinta-feira, 4 de dezembro de 2008
Arquimedes (287 a.C. - 212 a.C.)
Agora, bastava aplicar o método que descobrira. Mediu então a quantidade de água que transbordava de um recipiente cheio, quando nele mergulhava, sucessivamente, o volume de um peso de ouro igual ao da coroa, o volume de um peso de prata igual ao da coroa e o volume da própria coroa. Este, sendo intermediário aos outros dois, permitia determinar a proporção de prata que fora misturada ao ouro.
Essa passagem parece ser uma das muitas lendas que, desde a Antiguidade, envolveram a vida de Arquimedes. Na verdade, para resolver um problema daquele tipo, relativo à determinação do peso específico de um metal, ele precisava apenas aplicar o princípio que rege o fenômeno do empuxo (força vertical que empurra para cima um corpo imerso em um fluido). Esse princípio - que explica porque um navio flutua na água e porque um aeróstato sobe no ar - foi estabelecido por Arquimedes nos seus dois livros, Sobre os corposflutuantes, com os quais inaugurou um novo ramo da ciência física: a hidrostática. No primeiro daqueles dois livros, ele enuncia o princípio que se tornou conhecido como "princípio de Arquimedes": "Um sólido mais pesado que o fluido em que está imerso vai para o fundo do fluido, e se é pesado dentro do fluido ele será mais leve que seu verdadeiro peso, de um peso igual ao fluido deslocado".
Entretanto, essa conclusão não era, de modo algum, fruto de um súbito "estalo". Representava o coroamento de uma longa tradição científica que, desde o século VI a.C., desenvolvera as pesquisas matemáticas e buscava uma explicação racional para os diferentes fenômenos observados. A glória de Arquimedes consistiu, porém, em não apenas fazer avançar as matemáticas abstratas - ampliando as conquistas dos grandes matemáticos do passado, como Pitágoras, Tales, Árquitas de Tarento, Eudoxo e Euclides -, mas em ser igualmente um grande físico, engenheiro e técnico genial: inventava e fabricava aparelhos destinados às suas próprias pesquisas, e criava inclusive máquinas de guerra temíveis por sua efícácia. Representando o apogeu da ciência grega, é considerado o precursor do método experimental nas ciências fisico-matemáticas.
Parafuso de Arquimedes
Filho do astrônomo Fídias, Arquimedes nasceu em 287 a.C., em Siracusa, na Sicília, que então fazia parte da Grécia ocidental ou Magna Grécia. Embora os dados fantasiosos permeiem todos os informes sobre sua vida, parece certo que estudou em Alexandria (Egito), um dos grandes centros culturais da época. Ali teria conhecido Euclides, já velho, e seus discípulos imediatos; e o matemático Canon de Samos, de quem se tornou amigo. Não é certo, porém, que ali tivesse criado o chamado "parafuso de Arquimedes", empregado para retirar água das minas do Egito. Na verdade, esse aparelho já existia, ao que parece, há bastante tempo, sendo utilizado para tirar água do Nilo.
Reduzindo o equilíbrio de forças a um simples problema geométrico, estudou o equilíbrio dos sólidos, o funcionamento da alavanca e o movimento dos corpos celestes, além de ter organizado uma coleção - a mais completa da Antiguidade - de figuras planas com os centros de gravidade perfeitamente localizados. Além disso, também procurava utilidades práticas para suas descobertas. Extraordinário engenheiro, construiu, segundo depoimento de Cícero (106 - 43 a.C.), um planetário que reproduzia os diferentes movimentos dos corpos celestes; e um aparelho para medir as variações do diâmetro aparente do Sol e da Lua, um protótipo do modelo, mais requintado, que será construído pelo astrônomo Hiparco, no século II a.C.
Espelhos curvos queimam navios romanos
Atribui-se ainda a Arquimedes a idealização dos célebres "espelhos ustórios" (ustório = que queima, que facilita a combustão), espelhos curvos com os quais os defensores de Siracusa teriam queimado a distância - pela concentração dos raios solares - os navios romanos que sitiavam a região. Se tal fato pertence ao lado lendário de sua biografia, parece entretanto não haver dúvida de que Arquimedes, depois de colaborar com seus engenhos bélicos para a defesa de sua cidade natal, foi morto durante o massacre que se seguiu à tomada de Siracusa pelo cônsul romano Marco Cláudio Marcelo, em 212 a.C. Atendendo a um pedido do sábio, foi colocada em seu túmulo uma coluna na qual fora gravado um cilindro circunscrito a uma esfera, para comemorar a maneira pela qual calculou a área de uma superfície esférica.
Segundo consta, Arquimedes teria dito a Hierão: "Dêem-me um ponto de apoio e eu levantarei a Terra". Não era a pretensão de se comparar ao mitológico e super humano Héracles - que os romanos chamarão de Hércules -, divindade símbolo da força. Era a certeza matematicamente garantida - de que o princípio da alavanca, que ele havia estabelecido, representava extraordinário recurso prático para a multiplicação de uma força.
Página do Tratado da Quadratura da Parábola
Tradicionalmente, a geometria grega vinha investigando processos de transformação de figuras curvas em retas, equivalentes. A quadratura do círculo, por exemplo, constituía um problema que vários matemáticos procuraram resolver. Arquimedes dedicou-se profundamente a esse tipo de questão - e um dos seus principais livros sobre Matemática intitulou-se justamente Tratado da quadratura da parábola.
A transformação do curvilíneo em retilíneo é feita por Arquimedes através do chamado método "de exaustão". Se um triângulo é inscrito num círculo, sua área é tão claramente menor que a do círculo quanto a do triângulo circunscrito é maior. No entanto - eis o procedimento adotado por Arquirnedes - multiplicando-se o número de lados dessas figuras, as áreas dos polígonos formados, inscritos e circunscritos, já se aproximam mais da área do círculo. E com o multiplicar sucessivo dos lados, os polígonos assim formados apresentam áreas que crescem (para os inscritos) e diminuem (para os circunscritos), aproximando-se da do círculo, embora nunca coincidam com ela.
Arquimedes conseguiu ir multiplicando o número de lados dos polígonos até obter figuras de 96 lados; verificou que as áreas respectivas, apesar de cada vez mais próximas do círculo, eram sempre um pouco maiores ou um pouco menores. Havia aqui também um procedimento que subentendia a aproximação de um valor exato - a área do círculo; esta era um "limite" a ser atingido, uma "justa medida" que só permitia abordagens aproximadas.
O que estava implícito nesse método de resolução de um problema geométrico era - como no caso do estabelecimento do valor de "pi" - a existência de valores infinitesimais, que justificavam a gradativa variação de tamanhos e grandezas. Aqui também Arquimedes antecipa conquistas que a Matemática só efetivará plenamente no final do século XVII, com o cálculo infinitesimal de Leibniz e Newton.
A liberdade não era, porém, patrimonio de todos os gregos. Muitos eram escravos e, por isso, destituídos do direito de cidadania. O filósofo Aristóteles chega a afirmar que para alguns a escravidão era um fato natural e inerente à natureza dos indivíduos que, não possuindo certas capacidades. intelectuais de raciocínio abstrato (a "alma poética" para os gregos), deviam, como escravos, se ocupar apenas de atividades manuais.
Esse preconceito que, com raras exceções, era generalizado na sociedade escravista dos gregos, não poderia deixar de repercutir, além do campo propriamente político, no desenvolvimento da investigação científica e filosófica. O menosprezo pelas atividades manuais, exercidas por homens sem liberdade, foi certamente o fator decisivo para restringir a ciência grega ao nível quase exclusivamente teórico e para impedir o desenvolvimento da experimentação. A ciência deveria ser fruto do intelecto de homens livres e, portanto, capazes de especulação - e não o resultado de simples manipulações e experiências.
Poucos escaparam às limitações desse modo de pensar, que criava obstáculos à verificação empírica e bloqueava o campo das aplicações práticas dos conhecimentos teóricos. O próprio Arquimedes pagou tributo, ao que parece, a esse preconceito de natureza sócio-econômica. Embora precursor do moderno método experimental, e apesar de ter sido o maior engenheiro da Antigüidade, também ele considerava como suprema realização da inteligência humana as verdades científicas abstratas - que as matemáticas formulavam plenamente. Conta Plutarco que, quando solicitado a escrever um manual de engenharia, Arquimedes se negou, alegando que "considerava o trabalho de engenheiro, assim como tudo o que dissesse respeito às necessidades da vida, como algo sem nobreza e vulgar". Ele desejava que sua fama diante da posteridade fosse fundada inteiramente em sua contribuição à teoria pura. O que glorificou seu nome, entretanto, mais do que o cálculo de "pi" por aproximações sucessivas, foi o princípio fundamental da hidrostática, a que ele chegara pela mais simples observação da realidade.
terça-feira, 25 de novembro de 2008
Arquimedes
A maioria dos detalhes da vida de Arquimedes são desconhecidos. Sabe-se que nasceu em Siracusa, na época uma cidade-estado da Magna Grécia cerca de 287 a.C. Seu pai foi um astrônomo chamado Fídias, do qual nada se conhece. Quando jovem, estudou em Alexandria, o centro do saber da época, com Cônon, um dos discípulos de Euclides. Embora na Antiguidade não houvesse clara distinção entre matemáticos (geómetras), físicos (cientistas naturais) e filósofos, Arquimedes destacou-se ao longo da sua vida principalmente como inventor e matemático.
Arquimedes morreu após a tomada de Siracusa durante a Segunda Guerra Púnica, cerca do ano 212 a.C.. Foi morto por engano por um soldado romano, apesar dos soldados terem ordens explícitas para defendê-lo, já que os romanos tinham uma enorme admiração por ele. Diz-se que quando os soldados romanos invadiram a praia de Siracusa, encontraram um velho senhor - o próprio Arquimedes - desenhando círculos na areia. Sem imaginar que esse era o génio responsável pela criação das poderosas armas sicilianas, assassinaram-no quando ele se negou a obedecer a suas ordens, porque não queria ver perturbado o raciocínio que seguia nesse momento. De acordo com o seu desejo, a sua sepultura foi decorada com o desenho de uma esfera dentro de um cilindro, que fazia parte de uma das suas demonstrações matemáticas favoritas.
ARQUIMEDES 287ac à 212ac
domingo, 23 de novembro de 2008
Arquimedes
Jéssica Lazaro de Oliveira 2°B
Voltou mais tarde à sua terra natal.Foi considerado por muitos historiadores um dos maiores matemáticos de todos os tempos.
As principais obras de Arquimedes foram sobre:
☻A esfera e o cilindro
☻Os conóides e os esferóides
☻As espirais
☻A medida do círculo
☻A quadratura da parábola
☻O Arenário (contador de areia)
☻O Equilíbrio dos planos
☻Dos corpos flutuantes
☻O stomachion jogo geométrico
☻O problema dos bois
sábado, 22 de novembro de 2008
Euler na Matemática
Na área da Geometria, numa primeira abordagem, o seu reconhecimento deve-se ao uso das letras minúsculas a, b, c para os lados de um triângulo e das maiúsculas correspondentes A, B, C para os ângulos opostos, bem como a aplicação das letras r, R e s para o raio dos círculos inscrito e circunscrito e o semiperímetro do triângulo, respectivamente. Há a destacar, também, a “(...) bela fórmula (...)” (Boyer, 1974, p. 326):
4rRs = abc
que relaciona os seis comprimentos, referidos anteriormente, embora hajam resultados semelhantes na Geometria da Antiguidade.
No campo da Geometria Sintética o seu contributo não foi muito, apesar de actualmente se considerar a recta que contém o circuncentro, o ortocentro e o baricentro de um triângulo, como a recta de euler.Em Geometria Analítica fez-se notar, a partir de 1728, por usar coordenadas no espaço, por dar equações gerais para três grandes classes de superfícies – cilindros, cones e superfícies de revolução - e por definir o arco mais curto (geodésica) entre dois pontos de uma superfície cónica.
Análise e Cálculo
Os contributos de Euler no ramo da análise e do cálculo fizeram-se notar com a introdução de uma nova abordagem à resolução de equações diferenciais.
“Euler foi, sem dúvida, o maior responsável pelos métodos de resolução usados hoje nos cursos introdutórios sobre equações diferenciais, e até muitos dos problemas específicos que aparecem em livros de texto de hoje remontam aos grandes tratados que Euler escreveu sobre o Cálculo – Institutiones Calculi Differentialis (1755) e Institutiones Calculi Integralis (1768 – 1770, 3 volumes)”. (Boyer, 1974, p. 333)
Através destes quatro volumes, deu a conhecer o uso de factores integrantes, os métodos sistemáticos para resolver equações lineares de ordem superior com coeficientes constantes, bem como a distinção entre equações lineares homogéneas e não-homogéneas, e entre solução particular e solução geral. Foi, desde então, que se pode afirmar que o tratamento mais completo realizado na área do cálculo se deveu a Euler.
Probabilidades
O interesse de Euler pelo estudo das Probabilidades, impulsionado por Daniel (1700-1782) e Nicolaus Bernoulli, também se fez notar. Escreveu sobre expectativas de vida, o valor de uma anuidade, lotarias, entre outros aspectos da vida em sociedade e como seria previsível, contribuiu, também, com algumas notações.
Leonard Euler, o matemático.
Euler legou à posteridade um número assombroso de trabalhos sobre as mais diversas áreas, da Engenharia à Mecânica, da Óptica à Astronomia, da Música à Matemática (curvas, séries, cálculo de variações, cálculo infinitesimal, Geometria, Álgebra).
Produziu tanto durante a sua vida que durante quase 50 anos depois da sua morte, os seus artigos continuaram a ser publicadas na Academia de S. Petersburgo. A lista bibliográfica das suas obras, incluindo itens póstumos, contém 886 títulos. A sua pesquisa Matemática chegava a ser, em média, de 800 páginas por ano, durante toda a sua vida.
No tempo em que esteve em Berlim, Euler ganhou o hábito de escrever artigos e colocá-los numa pilha. Sempre que era necessário material para as publicações da Academia eram retirados artigos da mesma. Como a produção de Euler era superior às publicações, os artigos na base demoravam muito a ser publicados. Isso explica o facto de quando alguns artigos surgirem, extensões e melhorias dos mesmos já terem sido publicadas antes, com a assinatura de Euler.
Jamais algum matemático terá superado a produção deste homem.
quarta-feira, 19 de novembro de 2008
Exercícios sobre Prismas - Para Nota
55 - Qual é a área da base, a área lateral, a área total e o volume de um prisma reto de altura igual a 8 cm, cuna base é um triângulo retângulo de catetos 3 cm e 4 cm?
56 - A altura de um prisma triangular regular é igual a 10 cm. Calcule a área lateral, a área total e o volume desse prisma sabendo-se que o perímetro da base é igual a 18 cm.
59 - Um prisma triangular regular tem 4 cm de altura. Calcule o volume, sabendo-se que a aresta da base desse prisma mede 2 cm.
60 - A base de um prisma reto é um triângulo retângulo cujos catetos medem 5 cm a 12 cm. Calcule a área da base, a área lateral e a área total desse prisma cuja altura é igual a 10 cm.
61 - Calcule a diagonal, a área total e o volume de um paralelepípedo reto-retângulo de dimensões 2 cm, 4 cm e 6 cm.
64 - Se o volume de um cubo é 27 cm³, calcule a aresta e a área total desse cubo.
65 - Se a área total de um cubo é 150 m², calcule a aresta e o volume desse cubo.
Leonhard Euller
Como auxilio de Bernouli entrou para a academia de S.Peterburgo,fundada por Catarina I.Em 1730 passando a seção de filosofia por ocasião de morte de Nicolaus e afastamento de Daniel tornando-se o principal matematico já aos vinte e seia anos ,dedicou-se profundamente á pesquisa compondo uma quantidade inigulável de artigos inclusive para a revista de academia.
Em 1735 perdeu a visão do olho direito,mas suas pesquisas continuaram intensas chegando a escrever até mesmo enquanto brincava com seu filho
Ele foi o primeiro a tratar dos logaritimos como expoentes e com ideia correta sobre logaritimos de numeros negativos.
Francini athayde 2°B
sábado, 1 de novembro de 2008
Euller
Euller foi aluno de Jean Bernoulle e amigo de seus filhos Nicolaus e Daniel.
Com o auxílio de Bernoulli entrou para a academia de S. Petesburg,ocupando um lugar na seção de Medicina e Fisiologia, e em 1730 passando a seção de Filosofia por ocasião da morte de Nicolaus e afastamento de Daniel.Tornando-se o principal matemático já aos vinte e seis anos,dedicou-se profundamente à pesquisa compondo uma quantidade inigualável de artigos,inclusive para a revista da academia.
terça-feira, 21 de outubro de 2008
Vida de Eluer .
Assim Eluer recebeu seu primeiro mestrado aos seus 17 anos , mais tarde ele ganhou seu primeiro premio em uma competição numa academia de Paris , que assim ele conseguil ganhar por mais 12 vezes .
Mais em 1.735 ele perdeu a visão de um de seus olhos , assim ele teve qe se abituar e aprender a resolver as formulas mesmo ja a cada dia perdendo mais e mais de sua visão , terminando compretamente cego pelos seus 17 anos restante de sua vida , durante esse tempo sua produtividade somente almentou .
Eluer acabou morrendo vitima de um ''derrame'' aos seus 76 anos de idade , deixando assim a lembrança de um grande genio da Matamática :) .
Camila 2 ''B
quarta-feira, 8 de outubro de 2008
Probabilidade no dia a dia
Alguns conceitos importantes a compreender aqui são que se houver uma probabilidade de 20% que chova, há uma probabilidade de 80% que não chova. As probabilidades não podem adicionar até mais de 100%, e a soma de todas as várias possibilidades deve adicionar até 100%.
Em casos simples como uma aleta da moeda, ou na possibilidade da chuva, onde há somente 2 possibilidades, as 2 probabilidades adicionarão a 100%. Em algumas situações entretanto haverá mais de 2 possibilidades. Se nós calcularmos somente algumas das probabilidades, não adicionarão até 100%, porque nós não consideramos todas as possibilidades, mas aquelas possibilidades existem ainda, e devem adicionar até 100% no total.
Uma outra maneira escrever a mesma informação deve dizer que há uma probabilidade do 2 da chuva, e que há conseqüentemente uma probabilidade do 8 que não chova. A probabilidade total não pode ser mais de 1, e uma vez outra vez todas as possibilidades devem adicionar até 1.
Esses são alguns exemplos de onde usamos probabilidade em nosso dia a dia.
O que eu achei mais interessante foi Probabilidade, de acordo com minhas leituras, a probabilidade teve ínicio com os jogos de cartas, dados e de roleta. Esse é o motivo da grande axistência de exemplos de jogos de azar no estudo da probabilidade. A teoria da probabilidade permite que se calcule a chance de ocorrência de uma número em um experimento aleatório.
Permutação, Arranjo e Combinação
Probabilidade: Definição
Com a Probabilidade, é possível calcular a chance de determinado evento ocorrer.
Para resolvermos um problema de Probabilidade, podemos usar a fórmula:

Onde:
n(U) é o número de elementos do espaço amostral.
n(A) é o número de eventos.
Sendo assim, é só dividirmos o número de eventos pelo número de elementos do espaço amostral.
Abaixo, um exemplo:
Qual a probabilidade de:
Obtermos um número menor que 3 no lançamento de um dado?
Resolução:
n(U): 1,2 (os dois números menores que 3 que temos em um dado)
n(A): 6 (número de elmentos de um dado, seis números).
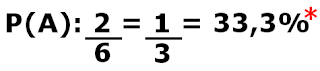
* Após fazer a divisão, multiplicamos o resultado por 100, para obtermos o por cento.
Resposta: A probabilidade de obtermos um número menor que 3 no lançamento de um dado é de 33,3%.
A ANÁLISE COMBINATÓRIA – Um resumo do 3º. Bimestre
Foi a necessidade de calcular o número de possibilidades existentes nos chamados jogos de azar que levou ao desenvolvimento da Análise Combinatória, parte da Matemática que estuda os métodos de contagem. Esses estudos foram iniciados já no século XVI, pelo matemático italiano Niccollo Fontana (1500-1557), conhecido como Tartaglia. Depois vieram os franceses Pierre de Fermat (1601-1665) e Blaise Pascal (1623-1662).
A ANÁLISE COMBINATÓRIA é um dos tópicos que a Matemática é dividida, responsável pelo estudo de critérios para a representação de quantidade de possibilidades de acontecer um agrupamento sem que seja preciso desenvolvê-los.
Na análise combinatória estudamos dentro do princípio fundamental da contagem:- Fatorial - Arranjos simples - Permutação simples - Combinação - Permutação com elementos repetidos
Um rapaz possui 4 bermudas e 4 camisetas. De quantos modos diferentes ele pode se vestir, com essas roupas?
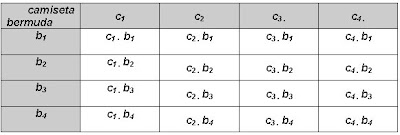 O quadro mostra que existem 4 . 4 = 16 modos diferentes para o rapaz vestir suas roupas.
O quadro mostra que existem 4 . 4 = 16 modos diferentes para o rapaz vestir suas roupas.Fatorial (!)
Sendo n um número natural maior que 1, definimos como fatorial de n (n!) o número:
n! = n .(n-1) . (n-2) . ... .4.3.2.1
Lê-se n! como n fatorial. Observe os exemplos a seguir: 7! = 7 . 6 . 5 . 4 . 3 . 2 . 1 = 5040 3! = 3 . 2 . 1 = 6 Por definição, para n = 0, temos 0! E, para n = 1, 1! = 1
Permutações com elementos repetidos
Portanto o número de anagramas da palavra BANANA é:
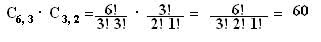
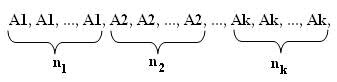 O número Pn (n1: n2: ...: nk) de permutações desse elementos será calculado por:
O número Pn (n1: n2: ...: nk) de permutações desse elementos será calculado por: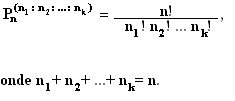
Arranjos Simples
Sendo A um conjunto com n elementos distintos e p um número natural, de modo que p ≤ n, denominamos de arranjos simples dos n elementos de A, tomados p a p, os agrupamentos ordenados de p elementos diferentes que é possível formar com os elementos de A. O número p é denominado de ordem ou classe do arranjo. Indicamos o número de arranjos de n elementos, p a p, por An,p ou Apn. A fórmula de arranjos simples é:

Combinações Simples
Sendo A um conjunto com n elementos distintos e p um número natural e modo que p ≤ n, denominamos de combinações simples dos n elementos, tomados p a p, os agrupamentos de p elementos distintos e que diferem entre si somente pela natureza de seus elementos. O número p é denominado classe ou ordem da combinação. O número de combinações simples, de classe p, de n elementos é denotado por Cn, p ou Cnp. A formula geral é:

Arranjo ou Combinação ?
Ao resolvermos uma situação problema de análise combinatória encontraremos um agrupamento, é nesse momento que aparece a seguinte dúvida: “esse agrupamento é uma combinação ou um arranjo?”.
É preciso identificar corretamente que tipo de agrupamento o exercício está trabalhando, para isso é possível utilizar o seguinte critério: Escrevemos um dos agrupamentos que o exercício sugere, mudamos a ordem dos seus elementos. A partir dessa mudança iremos concluir que:
• Será um arranjo se essa mudança alterar o agrupamento original, pois sabemos que um arranjo pode ser diferenciado tanto pela natureza de seus elementos como pela ordem desses elementos.
• Será uma combinação se essa mudança não alterar o agrupamento original, pois sabemos que uma combinação é um arranjo que se difere apenas pela alteração na natureza de seus elementos.
Veja o exemplo de como fazer essa verificação.
Exemplo: Um pintor, dispondo de cinco cores diferentes de tinta pretende misturar três delas, em quantidades iguais, para obter uma nova cor. Quantas novas cores ele poderá obter?
Verificando se os agrupamentos sugeridos são arranjos ou combinações: Vamos supor que as cinco cores que o pedreiro possui são: amarelo, branco, verde, vermelho, azul.
Escolhendo um dos agrupamentos formados pela combinação de 3 tintas teremos: {azul, amarelo, branco}, se mudarmos a ordem desses elementos {amarelo, branco, azul} não irá alterar o agrupamento, portanto os agrupamentos montados serão combinações simples. Pra encontrar a quantidade de combinações possíveis basta aplicar a fórmula:
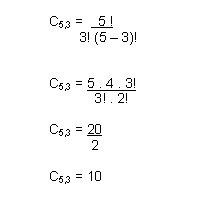
Portanto, é possível montar 10 combinações de 3 tintas com o grupo de 5 tintas
Probabilidades
As probabilidades são uma maneira diferente de expressar a mesma informação, mas em uma maneira que seja frequentemente mais aplicável ao poker e a outros jogos gambling.
Quando a probabilidade for expressada como um número decimal, ou uma porcentagem, as probabilidades estão expressadas como 2 números separados por uns dois pontos tais como 5:1. Pela convenção esta notação indica que as probabilidades são 5 a 1 de encontro a ocorrer do evento.
Há umas maneiras diferentes de dizer a mesma coisa, e de explicar o que os números significam. No exemplo, deixe-nos supõem que o evento que nós estamos interessados dentro está começando 1 cartão particular que nós necessitamos a fim fazer nossa mão. A notação diz-nos que 5 vezes nós não começaremos o cartão que nós necessitamos, e 1 vez, nós começaremos o cartão nós necessitamos. Usar-se que o mesmo exemplo, nós começará o cartão que nós necessitamos 1 vez em 6 tentativas, ou 1/6.
Probabilidade e cotidiano
O cálculo das probabilidades é utilizado em muitos ramos do conhecimento, mas principalmente na estatística, quando deseja se fazer interferências a respeito de uma população a partir de dados coletados numa amostra. Na Biologia, por exemplo, quando queremos saber previsões de caráter genético, na política ( previsões eleitorais) a probabilidade desempenha un papel importante.
Ex: Probabilidade Condicional ( Biologia )
Em alguns problemas de genética é preciso calcular a probabilidade de ocorrência de um evento sobre o qual já temos alguma informação.
Como nesse exemplo: Pais normais e heterozigotos , para o albinismo, tem uma criança normal. Qual a probabilidade de que essa criança seja heterozigota?
A criança em questão já nasceu e não é albina , certo? Então não podemos contar a probabilidade de ser aa , pois não tem essa possibilidade. Logo dos 3 encontros gaméticos possíveis temos 2/3 de ser heterozigota e 1/3 de ser AA.
DIFÍCIL.....
Tenho certeza que vocês podem se esforçar mais um pouco.
Esse assunto está muito difícil de ser entendido por leitores do blog. Que tal usar exemplos da vida diária? Alguns fizeram isso, parabéns!!!
Tentem pesquisar sobre o assunto e não coloquem fórmulas, pois sabem bem como elas são " chatas" quando não são muito bem entendidas.
Tem a pesquisa sobre os geômetras. MÃOS A OBRA.
Um abração a todos...
Sara
terça-feira, 7 de outubro de 2008
Vou fazer um breve comentário aqui sobre o que eu realmente entendi ,sobre os números binominais .
Sabemos que os números de combinações simples, de classe p, com N(numero) elementos é constituído , esse número também é chamado número binominal ou número combinatório.
um ex; as letras P/n são as chamadas de
binominal de N sobre P. (n)=n!
(p) p!(n-8)!
N é o numerador e P é o denominador.
Ou seja resumindo tudoo os dois números naturais que são N e P são os chamados de binominais que sempre indicamos por (P/N)
Já os complementares são distinguidos da seguinte forma , Ex: p+q=N
Ou seja eles são complimentares quando por ex ocorre 5/3 e 5/2
3+2=5 .
Ou seja resumindo tudo os dois números naturais são N e P , qe são chamados de binominais .
Bem assim termino meu assunto .
Postei aqui da maneira que eu entendi e espero qe vocês tmbem tenham se interesado e tenham intendido tambem .
Probabilidade
PERMUTAÇÃO SIMPLES e ARRANJO SIMPLES.
Permutação é um tipo de arranjo simples. Assim, relembrando que arranjo simples é um subconjunto de um conjunto A de n elementos. Os elementos que formam os arranjos podem se diferenciar pela natureza ou pela ordem de seus elementos.
fui isso que eu entendi de permutação simples e arranjo simples..
xauuu.....bjsssssss
permutaçao simples,e uma ato de permutar coisas ou seja mudar algo de ordem atraves
de contas!!!! que tambem e chamado de arranjo simples
No começo esse assunto foi um pouco dificil para mim ,mas aos poucos
consegui entender!!!
A permutaçao simples e tambem realizada por meio de sempre diminuir uma casa de um numero relacionado uma palavra por exemplo a palavra amor!!Quantos anagramas podemos formar com essa palavra??/ um todos podem pensar que e dificil mas nao e!!!veja como e feito!!!
bom primeiro fazemos tambem seu arranjo e nada mais nada menos que o ato de multiplicar seu numero de letras!!
AMOR=SAO 4 letras 4.3.2.1.=24,, este e seu arranjo!!!!!!!!!
E sua permutaçao seria
p={amor,amro,arom,armo,aorm.aomr,maro,maor,mroa,mrao,mora,moar,oamr,oarm,orma,oram,omar,omra,ramo
raom,rmoa,raom,roma,rmao,}e ha tambem sua formulade arranjo simples (An,p=n!
(n-p)!
Bom todos essas palavras sao suas permutaçoes!!!!foi isso que todos aluno do 2colegial aprenderam com a professora CAROLINA!!!!!
Probabilidade: Espaço amostral
Dados dois eventos A e B de um Espaço Amostral S a probabilidade de ocorrer A ou B é dada por: P(A U B) = P(A) + P(B) – P(A ∩ B) Verificação: O Número de elementos de A U B é igual à soma do número de elementos de A com o número de elementos de B, menos uma vez o número de elementos de A ∩ B que foi contado duas vezes (uma em A e outra em B).

∩ significa intersecção
U significa união
Análise Combinatória

O estudo da análise combinatória nos permite descobrir quais são as diferentes possibilidades de uma combinação de variáveis. Por exemplo, quantas placas de carro são possíveis de existir no sistema atual de placas brasileiro. É uma matéria bastante cobrada em vestibulares e concursos públicos, pois envolve um pensamento mais abstrato, pois na maioria das vezes, não enxergamos todas as possibilidades. A explicação dessa matéria é muito mais fácil quando utilizamos exemplos.
Então, supondo que um restaurante tenha disponível 2 tipos de bifes, 2 tipos de arroz, 2 tipos de feijão e 3 tipos de bebidas.
O dono do restaurante queira servir pratos contendo 1 elemento de cada tipo de comida. Nomeando os tipos de comida da forma "bife 1, arroz 1, arroz 2 ... bebida 1, bebida 2, etc",
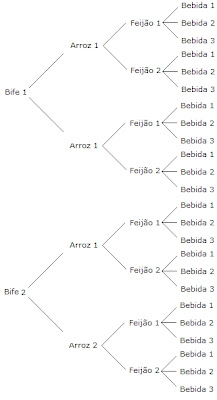
Mas podemos calcular de forma diferente. Basta multiplicar todas as opções de comida disponiveis: 2 . 2 . 2 . 3 = 24.
Análise Combinatória
Permutações
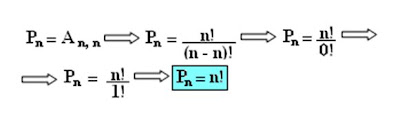
Os arranjos simples, de classe n, de n elementos distintos são denominados permutações simples desses n elementos.
Indicamos por Pn o número de permutações simples de n elementos:
Pn= n(n-1) . (n-2) . ... .3.2.1
e
P=n!
Permutações com elementos repetidos
A permutação de n elementos dos quais a são um tipo s de outro e b de outro, com a= s + b, é dada por:
P a,s,b ___n!___
n a! s! b!
Ex: Quantos anagramas tem a palavra BATATA?
____P6!____
P3.P2
____60!____= 60
3!2!
Sendo assim, a palavra BATATA tem 60 anagramas.
Arranjo Simples
São os agrupamentos ordenados diferentes que se podem formar com p dos n elementos dados.
Indica-se por An,p e Ap
n
Calculamos o total desses agrupamentos assim:
An,p = n. (n-1). (n-2). ... .(n-p-1)
ou
An,p =___n!___
(n-p)!
Combinação Simples
Combinação simples de n elementos tomados p a p ( com p menor ou igual a n) são os subconjuntos com exatamente p elementos que se podem formar com os números dados.
Indica-se por Cn,p o número total de combinações de n elementos. Calcula-se por:
Cn,p = ___n!___
p!( n-p)!
Permutação simples.
Permutações são os agrupamentos de um determinado número de elementos variando apenas a sua ordem. Ex.:
XYZ, XZY, YXZ, YZX,ZXY, ZYX.
O número de agrupamentos de uma permutação simples de n elementos é dado por n!.
P(m) = m(m-1)(m-2)...(m-p+1)...3.2.1
Ex.: De quantas formas podemos agrupar as sete cores do arco-íris? R: 7! = 5040
Como o uso de permutações é muito intenso em Matemática e nas ciências em geral, costuma-se simplificar a permutação de m elementos e escrever simplesmente:
P(m) = m!
Este símbolo de exclamação posto junto ao número m é lido como o fatorial de m, onde m é um número natural.
Embora zero não seja um número natural no sentido que tenha tido origem nas coisas da natureza, procura-se dar sentido para a definição de fatorial de m de uma forma mais ampla, incluindo m=0 e para isto podemos escrever:
0!=1
arranjos e combinaçoes
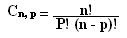
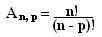
Hoje eu vou explica um pouco do que aprendi:
COMBINAÇÕES
Combinações:É sendo (A)um conjunto com(N)elementos distintos e (P)número natural e modo que (P)<(N),assim denominamos a combinação simples.
Exemplos:
1)Quantas equipes de 3 astronautas podem se formados com 20 astronautas?
resp: c,(n,p)= 6! = 6*5*4!=30 = 15
4!(6-4) 4!2! 2
è possivel formar 15 equipes de astronautas.
2) Numa prova de 10 questoes o aluno deve resolver apenas 6.De quantas maneiras diferentes ele poderá escolher essas 6 questões?
resp:C(n,p)= 30! = 30*29*28*27*26*25*24!= 142.506
6!(30-6)! 6! 24!
Os dois numeros 24 vc pode cortar eles,
nisso vc fatora o 6 e divide pela multiplicação de cima
essa sao as formulas a serem usadas
por combinação e arranjos simples
francini 2°B
sábado, 4 de outubro de 2008
PESQUISA
Obs: Como já era de costume: não vale tirar cópias da Internet, nem postar atividades iguais às dos colegas.
POSTEM SUAS PESQUISAS LOGO, POIS TALVEZ DÊ TEMPO DE SEREM COMPUTADAS NO 3º BIMESTRE.
Um abração a todos.
sexta-feira, 29 de agosto de 2008
Comentários
1) Grêmio 55% 2) Palmeiras 13% 3) Cruzeiro 12% 4) Botafogo 8% 5) São Paulo 3% 6) Vitória 3% 7) Flamengo 3% 8) Coritiba 3%
26 de Agosto de 2008 11:13
Cadê o Corínthians ????Dê sua opinião.
quinta-feira, 31 de julho de 2008
VAMOS CONTINUAR ALIMENTANDO.....
Quem se habilita?
Eu dou a dica, o conteúdo, e você dá a sua contribuição.
Estou contando com vocês, esse trabalho é muito especial para ser esquecido.
ANÁLISE COMBINATÓRIA E PROBABILIDADES ( próximo assunto)
Minha pergunta é: Qual é a chance do Palmeiras vencer o Campeonato Brasileiro ( série A) em 2008? e do São Paulo ? e do Corínthians ???
Dê sua opinião fazendo uma pesquisa e dê a resposta com coerência e clareza.
Estamos aguardando as colaborações.
Abraços
E o Internacional? tem alguma possibilidade????
quinta-feira, 26 de junho de 2008
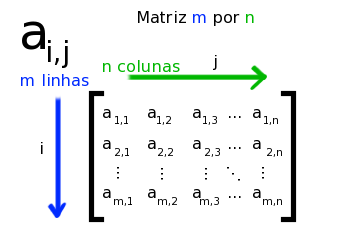 Toda imagem é formada por matrizes, toda matriz é no minimo de ordem 1x1 ou seja 1 linha e uma coluna, em imagens o tamanho da matriz esta relacionado a sua resolução,quanto mais linhas e culunas mais nitida sera a imagem .
Toda imagem é formada por matrizes, toda matriz é no minimo de ordem 1x1 ou seja 1 linha e uma coluna, em imagens o tamanho da matriz esta relacionado a sua resolução,quanto mais linhas e culunas mais nitida sera a imagem .Existem varios tipos matrizes existe matriz linha que é quando o número de colunas é igual a 1 .
E matriz coluna quando o número de linhas é igual a 1.
Ha a matriz quadrada , quando o número de linhas e colunas é igual.
Matrizes
Matrizes
Existem vários tipos de Matrize, por exemplo:
Matriz Quadrada:Quando o número de linhas é igual ao número de colunas.
Matriz Triangular:Quando os elementos da diagonal principal são todos nulos.
Matriz Diagonal:Quando a matriz quadrada de ordem n que é a linha, em que todos os elementos acacima e abaixo da diagonal principal são nulos.
Matriz Identidade:Quando a matriz quadrada de ordem n que é a linha, em todos os elementosda diagonal principal são iguais a 1 e os outros elementos são iguais a zero.
Matriz Nula:Quando o conjunto das matrizes tem os elementos iguais a zero.
Essas são uns dos exemplos de Matrizes, eu aprendi muito com os estudos das matrizes, eu achei muito importante, devemos saber sobre as Matrizes.
quarta-feira, 25 de junho de 2008
ONDE SÃO UTILIZADAS AS MATRIZES?
segunda-feira, 23 de junho de 2008
MATRIZES DETERMINANTES
Wollace Gomes n°35 ; Danilo Augusto n°09 2°B
Aplicações de matrizes e determinantes.
Matriz quadrada é a que tem o mesmo número de linhas e de colunas (ou seja, é do tipo mxn).
A toda matriz quadrada está associado um número ao qual damos o nome de determinante.
Dentre as várias aplicações dos determinantes na Matemática, temos:
-resolução de alguns tipos de sistemas de equações lineares;
-cálculo da área de um triângulo situado no plano cartesiano, quando são conhecidas as coordenadas dos seus vértices.
Estudo das Matrizes
Essas matrizes não são só em computadores são usadas também em qualquer empresa ou residÊncia para armazenar dados.
Matriz triangular: é quando os elementos acima ou abaixo da diagonal principal são todos nulos.
Ex.:2 0 0
8 3 0
7 9 -5
Matriz identidade: quando os elementos da diagonal principal são iguais a 1 e os outros iguais a 0.
Ex.:I³=1 0 0
0 1 0
0 0 1
Matriz nula: é quando todos os elementos iguais a zero denomina-se matriz nula.
Ex.:A-A
2 0 0 2 0 0 0 0 0
0 4 0 - 0 4 0 = 0 0 0
0 0 6 0 0 6 0 0 0
Determinante de matriz quadrada de ordem 1:seja a matriz quadrada de ordem 1,indicada por A=[A¹¹]..Por definição,o determinante de A é igual ao número A¹¹.Indicamos assim:Det A=A¹¹
Por exemplo dada as matrizes A=[4] e B=[-2] escrevemos Det A=4;Det B=-2;Det A + Det B=4+(-2)=2.
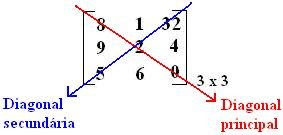
Determinante de matriz quadrada de ordem 2: se A é uma matriz quadrada de ordem 2,calculamos seu determinante fazendo o produto dos elementos da diagonal principal menos o produto dos elementos da diagonal secundária.
Ex.:Det A=6 3 =6.(-4)-2.3=-24-6= -30
2 -4
Determinante de matriz quadrada de ordem 3:consideremos a matriz de ordem 3
A¹¹ A¹² A¹³
A= A²¹ A²² A²³
A³¹ A³² A³³
Define-se o determinante da matriz de ordem 3 ao número:
A¹¹ A¹² A¹³
Det A= A²¹ A²² A²³=A¹¹A²²A³³ + A¹²A²³A³¹ + A¹³A²¹A³² - A¹³A²²A³¹ - A¹¹A²³A³² - A¹²A²¹A³³
A³¹ A³² A³³
Ex.: 3 1 5 3 1 5 3 1
A=2 0 -2 2 0 -2 2 0
-1 4 -3 -1 4 -3 -1 0
0+24+6 0+2+40=72
Det A=72
Ex.:DP DS (A).(B+1) (B).(A+1)
A A+1 AB+1A - AB-1B
B B+1 A-B
domingo, 22 de junho de 2008
A diferença entre a TV normal e a digital
Em outra linguagem menos tecnica,quando vc estiver vendo tv Comum chegue bem pertinho dela e vc vai perceber um tanto de quadradinhos que são chamadas de matrizes muitos retangulos impossivel de contar.Na tv digital ha muito mais quadradinhos por isso ela oferece melhor imagem!
sexta-feira, 20 de junho de 2008
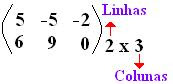
M x N ( lê-se m por n).
Obs.:
1- se em uma matriz o número de linhas é diferente do número de colunas então a matriz será dita como retangular (m ¹n).
2- se em uma matriz o número de linhas é igual ao de colunas então a matriz será dita quadrangular (m = n) onde formam a diagonal principal da matriz.
3 – Uma matriz apenas é igual a outra se todos os seus elementos forem iguais e ocuparem as mesmas posições dos elementos da segunda.
Matrizes Importantes:
1-) Matriz transposta: é aquela onde as linhas se transformam em colunas e as colunas em linhas.
2-) Matriz oposta é aquela onde todos os elementos possuem sinais trocados.
3-) Matriz nula: é aqueles onde todos os elementos são iguais a 0 (zero).
4-) Matriz identidade ou unidade: é uma matriz quadrada onde os elementos da diagonal principal são todos iguais a 1 e os demais 0 (zero).
5-) Matriz diagonal: é uma matriz quadrada onde os elementos fora da diagonal principal são todos iguais a 0 (zero).
OBS: Matriz singular: é uma matriz diagonal onde os elementos da diagonal principal são todos iguais.
6-) Matriz triangular: é matriz quadrada onde todos os elementos acima ou a baixo da diagonal principal ou secundária são todos iguais a 0 (zero).
7-) Matriz linha: é aquela que possui apenas uma linha.
8-) Matriz coluna: é aquela que possui apenas uma coluna.
9-) Matriz simétrica: uma matriz quadrada é dita simétrica se ela é igual a sua transposta.
10-) Matriz anti-simétrica: uma matriz quadrada é dita anti-simétrica se sua oposta é igual a sua transposta
A Matriz é usada para da um resolução melhor,quanto mais m x n melhor a resoluçaõ da imagem, quanto menos m x n pior a resolução da imagem.
quinta-feira, 19 de junho de 2008
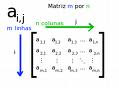
A Matriz é uma tabela de elementos dispostos segundo linhas e colunas, sendo m o número de linhas, e n o número de colunas.
Um elemento qualquer é representado por aij onde i representa a linha e j a coluna, onde o elemento se encontra localizado.
Uma matriz recebe certo tipo de nome dependendo da quantidade de elementos em suas linhas e colunas ou apenas por características específicas:
►Matriz linhas: quando é apenas formado por uma linha.
►Matriz coluna: quando é apenas formado por uma coluna.
►Matriz quadrada: quando tem a mesma quantidade de linhas e colunas.
►Matriz diagonal: quando todos os números que não estão na diagonal principal forem zero.
►Matriz identidade: quando numa matriz quadrada os números da diagonal principal forem zero, e o restante zero.
►Matriz oposta: quando troca apenas o sinal das matrizes.
►Matrizes iguais ou igualdade de matrizes: quando todos os elementos forem iguais.
Kely_2ºC
quarta-feira, 18 de junho de 2008
DNA
TEMOS MAIS UM ENCONTRO MARCADO NO SÁBADO, POIS NOSSAS EQUIPES SE CLASSIFICARAM PARA RESOLVER O ENIGMA FINAL.
ESTOU AGRADECENDO A TODOS OS PAIS, MÃES, AMIGOS, TIOS, TIAS ETC... QUE PARTICIPARAM DE ALGUMA MANEIRA DESSE DESAFIO ( ALGUNS FIZERAM COMIDA, OUTROS NÃO DORMIRAM, ALGUNS FIZERAM UMA OU DUAS QUESTÕES QUE FORAM DECISIVAS NA CLASSIFICAÇÃO DAS EQUIPES)
UM AGRADECIMENTO ESPECIAL A FAMÍLIA DA PROFª JUSCELINA ( FAMÍLIA MUSICAL) QUE FOI DE GRANDE VALIA NA RESOLUÇÃO DA ETAPA - MÚSICA.
ESPERO QUE ESSE SEJA O PRIMEIRO DE MUITOS DESAFIOS QUE ESTÃO POR AÍ. TODOS MOSTRARAM QUE TEM GARRA E COMPETÊNCIA PARA A CLASSIFICAÇÃO FINAL, A NÍVEL NACIONAL.
sábado, 14 de junho de 2008
Matriz
Ex.: uma foto.
Quanto mais linhas e colunas ela tiver maior vai ser sua resolução (clareza).
M e N: são dois números inteiros maiores ou igual a 1.
M: linhas {M.N}
N: colunas
Exemplo de uma matriz:
Matriz de ordem 2x2
[A¹¹ A¹²]
[A²¹ A²²]
Duas linhas e duas colunas.
Jéssica Costa de Oliveira
Serie: 2ºB
sexta-feira, 13 de junho de 2008
bom matrizes nao esta so relacionada so com contas !!!!!!!!
as novas tvs tembem sao exemplos de que matrizes tambem esta relacionada a esse assunto !!
bom matrizes e usada na resoluçao de maquinas ftograficas e celulares !!!!!!
todo mundo que tem um celular pensaipq tem aqueles numeros atra do celular tipo 360x140!!
bom.. isso esta relacionda com matriz pq e com ela que a foto fica melhor ou ruim dependendo de quanto pixel ou existe!!
a tv convencional tem 525 pixel masso 483 chegam nas nosas casas!!o resto e perdido pela ma tranmissao!!!
As niovas tvs terao GPS!!!para evitar uma mal transmissao!!!mesmo sendo digitais ainda sim carregam consigo as matrizes poi preisa delas para a imagem pq ela tera cores diferentes ou seja melhores e cada quadradinho mudara de angulo para um aspcto melhor!!!
assim caminharemos a um futuro brilhante das inovadoras tvs digitais!!!
Matrizes
.jpg)
Veja um video para esclarecer mais o assunto:http://www.youtube.com/watch?v=seY_fe-CjIk
Outros exemplos:
O crescente uso dos computadores tem feito com que a teoria das matrizes seja cada vez mais aplicada em áreas como Economia, Engenharia, Matemática, Física, dentre outras.
Nome:Gabriele Piaati 2°A
quinta-feira, 12 de junho de 2008
matrizes
Matrizes
Esta imagem abaixo também está sendo formada por linhas e colunas, cada pontinho dela é um valor da matriz.

segunda-feira, 9 de junho de 2008
MATRIZES
ESSE CONTEUDO É SOBRE AS MATRIZES ELA BEM REPRESENTA A EQUAÇÃO DO DO 2°ANO NELA EU VOU EXPLICAR O QUE EU ENTENDI:
MATRIZES:SAO FEITAS DE COLUNAS E LINHAS,QUANDO TIVEMOS MATRIZES LINHAS OU MATRIZES COLUNAS TAMBÉM PODEMOS CHAMÁ-LOS DE VETORES.
NELAS TEMOS VARIO TIPOS DE MATRIZES COMO:
MATRIZ QUADRADA
MATRIZ TRIÂNGULAR
MATRIZ DIAGONAL
MARIZ IDENTIDADE
MATRIZ NULA
ESSAS SÃO EXEMPLOS DE ALGUMAS MATRIZES QUE EU SEI MAS EXISTEM MUITO MAIS TIPOS
ELAS SÃO MUITO USADOS PARA PREENCHER ESPAÇOS DE UM DEZENHO NO COMPUTADOR.
MEU NOME É FRANCINI DO 2°B
JESSICA NOGUEIRA 2ºB
sexta-feira, 16 de maio de 2008
SARA ESTE ANO ESTAMOS INOVANDO AS AULAS
DE MATEMATICA!!!!
AULAS MAIS PRODUTIVAS ESTAO SENDO DADAS P OS ALUNOS
estou começando a me entender com as aulas de matematica
esse blog so serviu para estimular o que ja havia sendo feito pela sara
esse ano acho que sera o melhor de todos!!!!!
e isso so ira me ajudar cada dia mais e mais!!!!!
estou ate gostando ate um pouco da materia
que antes para mim era muito
confusa e complicada!!!!!!
mas hoje sei que com sua ajuda
serei melhor em matematica.
obrigada!!!!!!
quinta-feira, 15 de maio de 2008
Planetário.
Vejam o que descobri:
Júpiter é o quinto planeta a partir do Sol e o maior de todos:
distância do Sol: 778.330.000 km (5,20 u.a)
diâmetro equatorial: 142.984 km; diâmetro polar: 133.708 km
massa: 1,900e27 kg
Júpiter tem duas vezes mais massa que todos os outros planetas juntos (318 vezes a massa da Terra). Júpiter é o quarto objeto mais brilhante no céu (depois do Sol, Lua e Vênus; em alguns períodos, Marte é também mais brilhante). É conhecido desde os tempos pré-históricos. A descoberta de Galileu, em 1610, das quatro luas de Júpiter, Io, Europa, Ganimédes e Calisto (hoje conhecidas como luas Galileanas), foi a primeira constatação de um centro de movimento que, claramente, não estava centrado na Terra. Esse foi um ponto significativo a favor da teoria heliocêntrica de Copérnico; Por defender abertamente a teoria de Copérnico, Galileu foi aprisionado a mando da Inquisição, forçado a abjurar suas crenças e condenado ao cárcere pelo resto de sua vida.
Júpiter foi visitado pela primeira vez pela sonda Pioneer 10 em 1973 e, mais tarde, pelas sondas Pioneer 11, Voyager 1, Voyager 2 e Ulysses. A sonda Galileu está atualmente viajando em direção à Júpiter. Os planetas gasosos não têm superfícies sólidas, seu material gasoso simplesmente tornar-se mais denso com a profundidade (os raios e diâmetros dos planetas são para níveis correspondentes a uma pressão de 1 atmosfera). O que vemos quando olhamos para esses planetas é o topo das nuvens em suas atmosferas (ligeiramente acima do nível de 1 atmosfera). Júpiter é cerca de 90% hidrogênio e 10% de hélio, com traços de metano, água, amônia e "rochas". Isso aproxima-se muito da composição da Nebulosa Solar primordial da qual todo o sistema solar se originou. Saturno tem uma composição similar, mas Urano e Netuno têm muito menos hidrogênio e hélio. Nosso conhecimento do interior de Júpiter (e de outros planetas gasosos) é essencialmente indireto, e é provável que permaneça assim por muito tempo. A sonda atmosférica Galileu penetrará apenas até próximo ao nível de 25 bar antes de perder contato com a Terra. Júpiter provavelmente tem um núcleo de material rochoso, algo em torno de 10 a 15 massas terrestres. Acima do núcleo fica o principal constituinte da composição do planeta - hidrogênio metálico em forma líquida. Essa forma exótica do mais comum dos elementos é possível somente a pressões superiores a 4 milhões de bars, como é o caso das camadas interiores de Júpiter (e Saturno). O hidrogênio metálico líquido constitui-se de elétrons e prótons ionizados (como o interior do Sol, mas a uma temperatura bem mais baixa). À temperatura e pressão do interior de Júpiter, o hidrogênio é um líquido, não um gás. É um condutor elétrico e a fonte do campo magnético de Júpiter. Essa camada provavelmente também contém alguma quantidade de hélio e traços de vários "gelos".
1º BIMESTRE .
E para melhor compreendermos, o livro nos propõe que façamos o estudo das razões trigonométricas através do círculo trigonométrico, o qual fizemos juntamente com a professora em sala de aula. E foi utilizando o círculo trigonométrico, que pudemos construir os gráficos do seno e cosseno.
Neste bimistre também aprendemos: Raio, Radiando, Comprimento da circunferência, Área da circunferência, e vários outros elementos da trigonometria. Quase toda a matéria do livro nos aprendemos, foram poucas coisas que não chegamos a ver.
Particularmente, gostei muito da maneira de ensinar da Profª Sara, conseguiu nos passar as informações mais importantes, de uma maneira resumida.
quarta-feira, 14 de maio de 2008
Pois a Professora Sara está tirando a rotina das aulas e sempre inovando, sempre mudando sua aula, e assim não ficando repetitiva as aulas o que anima muito os alunos, até alunos que não faziam nada estão fazendo, todos aprendem muito na aula da Sara, são poucos os professores hoje em dia que tem tanta qualidade pra fica inovando nas aulas, toda aula tem coisa nova, um dia é na informática, outro na sala de aula, mas com lições diferentes e assim por diante.
Em minha opinião na sala de informática é onde os alunos mais aprendem e participam das aulas, e assim a qualidade intelectual dos alunos só crescem, estou aproveitando muito nas aulas de Matemática
Aulas de matemática
tudo o que está no livro.
Exemplos:Graus,triangulos,lados,radianos,angulos e etc.
E com as explicações da professora e do circulo trigonométrico consequimos aprender,e a compriender tudo o que foi explicado.
Excelente trabalho!
A utilização desses novos meios é importantíssima dando uma aula mais dinâmica, interessante, deixando de lado aquele “bicho de sete cabeças” como é conhecida por alguns a matemática.
circulo trigonométrico
O circulo trigonométrico é passa por dois eichos chamados de eicho x e eicho y cos é o eicho x e sen é o eicho y para sabe a medida da circunferencia precisamosdos angulos que são 30,45,60,90 e vai até 360 paraq voce sabem as medidas dos anguloas voce precisa das formulas do sen e do cos.
Aulas de Matematica 1°Bimestre!!
No 1° Bimestre nós aprendemos muitas coisas interessantes e Revisamos outras..apesar da nossa classe não ser muito comportada, deu pra tirar duvidas sobre Trigonometria, sobre o PI radiano, Arcos trigonométricos pois eu tinha varias duvidas na 8° serie e no 1° colegial.. A professora tem muitos jeitos de dar aulas divertidas, eu aprendi me divertindo na sala, e isso foi muito bom, pois deu para tirar duvidas..Nós fomos para a Informática,eu gostei de Mexer no Programa Cabri Geometre,apesar de ainda não saber mexer direito. Mas eu gostei muito pois nós só ficávamos na sala, e isso muitas vezes era chato pois são 6 aulas por dia 6 aulas na classe ninguém merece, mas com a oportunidade de sairmos da sala e ir pra Informática era muito divertido. Eu gostei pois alem de tudo isso eu aprendi varias coisas que me ajudarão na hora de fazer um Vestibulinho, um ENEN.. E em nossas Vidas pois a matemática esta em tudo. .
Eu espero que no 2° Bimestre seja tão bom quanto o 1°..
Sobre as aulas de matemática...
Bom, esse bimestre trabalhamos várias coisas, primeiro começamos com o jornal, apesar de ser muito complicado, com as explicações em sala de aula sobre: Crescimento, decrescimento, proporcionalidade; Grandezas proporcionais e representações gráficas; Relacionando e analisando grandezas (tabelas); Análise e interpretação de gráficos; Função afim; Função quadrática; Simetria; Inequações; etc, consegui aprender e fazer uma boa prova. Assim que terminamos as atividades do jornal começamos as atividades do livro, em muito pouco tempo conseguimos trabalhar 55 páginas e aprendemos muito também, estudamos : ângulos, seno, cosseno, tangente, medida da circunferência, radiano, gráficos das funções seno e cosseno, além disso que aprendemos em sala de aula, fomos para sala de informática e lá reforçamos o conteúdo dado em sala de aula com os gráficos feitos no Cabri Geometre, isso fez com que as aulas não ficassem cansativas, chatas e nos trouxe muitos benefícios em relação ao aprendizado.
Comentário por: Felipe - 2º B
Função quadrátitca
que nós trabalhos muito também foi função quadrática.
Função quadrática é uma função dada por f(x) = ax2 + bx + c,
nas aulas de informatica fizemos bastante graficos relacionado
a isso, aprendi que grafico de uma função quadrática é chamado de "Parábola",
que é um desenho que forma com a concavidade virada para cima ou para baixo.
lembrando que se, * a>0, a parábola tem a concavidade voltada para cima; e se
*a<0 , a parábola tem a concavidade voltada para baixo
Para conseguimos fazer um grafico desse, temos que Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida, ligamos os pontos assim obtidos.
Bom, foi isso que eu entendi, sobre os graficos de funções quadráticas.
.jpg)

